浮点数的二进制表示

本文主要讨论下计算机如何将浮点数存储在有数量限制的内存中。

如何表示二进制小数

假设我们有 16 位（2 个字节）来存储数字。在 16 位中，我们可以存储以下范围内[0, 65535]整数：

(0000000000000000)₂ = (0)₁₀

(0000000000010001)₂ =
    (1 × 2⁴) +
    (0 × 2³) +
    (0 × 2²) +
    (0 × 2¹) +
    (1 × 2⁰) = (17)₁₀

(1111111111111111)₂ =
    (1 × 2¹⁵) +
    (1 × 2¹⁴) +
    (1 × 2¹³) +
    (1 × 2¹²) +
    (1 × 2¹¹) +
    (1 × 2¹⁰) +
    (1 × 2⁹) +
    (1 × 2⁸) +
    (1 × 2⁷) +
    (1 × 2⁶) +
    (1 × 2⁵) +
    (1 × 2⁴) +
    (1 × 2³) +
    (1 × 2²) +
    (1 × 2¹) +
    (1 × 2⁰) = (65535)₁₀

如果我们需要一个有符号整数， 最高位表示符号,0 为正,1 为负。在这种情况下，16 位整型数据的取值范围是[-32768, +32767]。

这时我们可以看出，这种方法不允许表示浮点数（如：27.15625），下面我们来看看浮点数 27.15625 用二进制如何表示：
整数部分

(27)₁₀ = (11011)₂

小数部分，我们按照乘 2 余 1 法则，将十进制小数转为二进制小数：

0.15625 * 2² = 0.3125; // < 1
0.3125 * 2 = 0.625;   // < 1
0.625 * 2 = 1.25;     // > 1
0.25 * 2 = 0.5;       // < 1
0.5 * 2 = 1;          // = 1

则 0.15625 转换成二进制：00101

(0.15625)₁₀ = (0 x 2⁻¹) + (0 x 2⁻²) + (1 x 2⁻³) + (0 × 2⁻⁴) + (1 × 2⁻⁵)

现在，我们可以得到看上去有点像的二进制的小数：

(27.15625)₁₀ = (11011.00101)₂
(27.5)10 = (11011.1)₂

但是这里小数点并不能被计算机处理，计算机认识 0 和 1。所以，我们需要进一步处理，将符号、小数点也数字化，基本思路就是：

• 0 表示正数，1 表示负数，将符号 1，0 数字化；
• 用科学计数将小数整数化；

下面我们以 IEEE754 为例，我们看下十进制浮点数如何表示成二进制浮点数进行存储。

IEEE 754 标准

IEEE，电气和电子工程师协会( 全称是 Institute of Electrical and Electronics Engineers)是一个国际性的电子技术与信息科学工程师的协会，是目前全球最大的非营利性专业技术学会，IEEE 754 标准是 IEEE 二进位浮点数算术标准（IEEE Standard for Floating-Point Arithmetic）的标准编号。
根据国际标准 IEEE 754，任意一个二进制浮点数 V 可以表示成下面的形式：

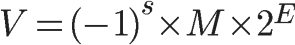
也就是浮点数的实际值，可以分为三个部分：

• (-1)^s 表示符号位，当 s=0，V 为正数；当 s=1，V 为负数。
• M 表示有效数字，大于等于 1，小于 2。
• 2^E 表示指数位。

举例来说：

十进制的 5.0，写成二进制是 101.0，相当于 1.01×2^2。那么，按照上面 V 的格式，可以得出 s=0，M=1.01，E=2。
十进制的-5.0，写成二进制是-101.0，相当于-1.01×2^2。那么，s=1，M=1.01，E=2。

5.0 -> 101.0 -> (-1)⁰ * 1.01 * 2²
-5.0 -> -101.0 -> (-1)¹ * 1.01 * 2²

IEEE 754 对有效数字 M 和指数 E，还有一些特别规定。
前面说过，1≤M<2，也就是说，M 可以写成 1.xxxxxx 的形式，其中 xxxxxx 表示小数部分。IEEE 754 规定，在计算机内部保存 M 时，默认这个数的第一位总是 1，因此可以被舍去，只保存后面的 xxxxxx 部分。比如保存 1.01 的时候，只保存 01，等到读取的时候，再把第一位的 1 加上去。这样做的目的，是节省 1 位有效数字。以 32 位浮点数为例，留给 M 只有 23 位，将第一位的 1 舍去以后，等于可以保存 24 位有效数字。

至于指数 E，情况就比较复杂。

首先，E 为一个无符号整数（unsigned int）。这意味着，如果 E 为 8 位，它的取值范围为 0~255；如果 E 为 11 位，它的取值范围为 0~2047。但是，我们知道，科学计数法中的 E 是可以出现负数的，所以 IEEE 754 规定，E 的真实值必须再减去一个中间数，对于 8 位的 E，这个中间数是 127；对于 11 位的 E，这个中间数是 1023。

比如，2^10 的 E 是 10，所以保存成 32 位浮点数时，必须保存成 10+127=137，即 10001001。

然后，指数 E 还可以再分成三种情况：

1. E 不全为 0 或不全为 1。这时，浮点数就采用上面的规则表示，即指数 E 的计算值减去 127（或 1023），得到真实值，再将有效数字 M 前加上第一位的 1。

2. E 全为 0。这时，浮点数的指数 E 等于 1-127（或者 1-1023），有效数字 M 不再加上第一位的 1，而是还原为 0.xxxxxx 的小数。这样做是为了表示 ±0，以及接近于 0 的很小的数字。

3. E 全为 1。这时，如果有效数字 M 全为 0，表示 ± 无穷大（正负取决于符号位 s）；如果有效数字 M 不全为 0，表示这个数不是一个数（NaN）。

一般来说，现在的编译器都支持两种浮点格式，一种是单精度，一种是双精度。单双精度分别对应于编程语言当中的 float 和 double 类型。其中 float 是单精度的，采用 32 位二进制表示，其中 1 位符号位，8 位阶码以及 23 位尾数。double 是双精度的，采用 64 位二进制表示，其中 1 位符号位，11 位阶码以及 52 位尾数，js 中的浮点数就是双进度的。如下表所示：

数据类型	符号位	阶码	尾数	总位数	偏移值
单精度	1	8	23	32	127
双精度	1	11	52	64	1023

为了更好地了解 IEEE 754 标准的工作原理。为简单起见，这里使用 32 位数字，但同样的方法也适用于 64 位数字。

还是开头的例子，我们把十进制浮点数(27.15625)转换成二进制，如下：

(27.15625)₁₀ -> (11011.00101)₂ -> 1.101100101 * 2⁴;

1. 符号位： 正数，s = 0,
2. 阶数为4，则阶码 = 4 + 127 = 131 = (1 × 2⁷) + (1 × 2¹) + (1 × 2⁰) = 10000011
3. 尾数，101100101，不足23位，右侧补0。

最终结果如下：
0 10000011 10110010100000000000000

示例图：

下面我们再看一个列子，把(-10.15)转换成二进制，如下：

(10.15)₁₀ -> (1010.0010011001...1001...)₂ -> 1.0100010011001...1001... * 2³;

1. 符号位： 负数，s = 1,
2. 阶数为3，则阶码 = 3 + 127 = 130 = (1 × 2⁷) + (1 × 2¹) = 10000010
3. 尾数，0100010011001...1001...，尾数部分是01000+n个1001无限循环小数，由于存储位数限制，只能是 23位，因此第24位0要进行舍去操作，1入0舍。

最终结果如下：
1 10000010  01000100110011001100110

示例图：

转换工具

这里有个网址，可以方便查看十进制、二进制、十六进制与单精度、双精度、四精度之间的关系：(https://babbage.cs.qc.cuny.edu/IEEE-754/)

0.1+0.2!=0.3

最后来看看 0.1+0.2!=0.3 这个经典问题。
我们 javascript 为例，其浮点数是 64 位。

x = (0.1)₁₀ = (0.000110011...0011...)₂ = 1.10011...0011... * 2⁻⁴;

那么x阶数：-4，则阶码 = 1023 + (-4) = 1019 = 01111111011;

x的尾数：10011...0011...;

所以最终：
x = 0 01111111011 1001100110011001100110011001100110011001100110011010

同理：

y =  (0.2)₁₀ = (0.00110011...0011...)₂ = 1.10011...0011... * 2⁻³;

那么x阶数：-3，则阶码 = 1023 + (-3) = 1020 = 01111111100;

y的尾数：10011...0011...;

所以最终：
y = 0 01111111100 1001100110011001100110011001100110011001100110011010

浮点数运算

浮点数的加减运算一般由以下五个步骤完成：对阶、尾数运算、规格化、舍入处理、溢出判断

对阶

x的阶码 = 01111111011;

y的阶码 = 01111111100;

y-x 阶码 = 01111111100 - 01111111011 = 1

则x的阶码需要+1，尾数需要向右移动一位，采用舍入法则，末尾0舍去，如下

x = 0 01111111100 1100110011001100110011001100110011001100110011001101
y = 0 01111111100 1001100110011001100110011001100110011001100110011010

尾数运算

x:  0.1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1101
+y: 1.1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010
----------------------------------------------------------------------
   10.0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0111

规格化

简单理解就是尾数是否是 1.xxxxxx 这种格式，目前是 10.xxx，因此需要做规格化处理，即尾数需要右移 1 位（也称右规），同时阶码+1，如下：

// 尾数右移
1.00110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 011(1);

// 阶码+1
0 01111111101 0011001100110011001100110011001100110011001100110011(1);

规格化后，尾数高位 1，隐藏不显示。

舍入处理

规格化时，尾数末位如果是 1，直接移除将会丢失进度，因此需要舍入处理，通常采用“1 入 0 舍”法，本例尾数末位是 1，因此需要“入”，即+1 处理：

0 01111111101 0011001100110011001100110011001100110011001100110011(1);
0 01111111101 0011001100110011001100110011001100110011001100110100;

溢出判断

结果：0 01111111101 0011001100110011001100110011001100110011001100110100，没有溢出，阶码不调整，所以 0.1+0.2 的结果为：

0 01111111101 0011001100110011001100110011001100110011001100110100

转为 10 进制：

0 01111111101 0011001100110011001100110011001100110011001100110100
= (-1)⁰ * 2⁻² * (2⁰ + 0.2000000000000002)
= 0.30000000000000004

参考文献

• https://trekhleb.dev/blog/2021/binary-floating-point/
• https://babbage.cs.qc.cuny.edu/IEEE-754/