十一、JavaScript专题之数组乱序

发表于 分类于 阅读次数：

引言

数组乱序指的是：将数组元素的排列顺序随机打乱。
通常我们在做抽奖系统或者发牌等游戏时，会遇到数组乱序的问题。 举个例子：将 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 乱序。

sort 结合 Math.random

先看代码实现：

1
2
3
4
5
var arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
arr.sort(function () {
  return Math.random() - 0.5;
});
console.log(arr);

Math.random() - 0.5 随机得到一个正数、负数或是 0，如果是正数则升序序排列，如果是负数则降序排列，如果是 0 就不变，然后不断的升序或者降序，最终得到一个乱序的数组。
乍一看，这似乎是一个合理的解决方案。事实上这种方式并不是真正意思上的乱序，一些元素并没有机会相互比较， 最终数组元素停留位置的概率并不是完全随机的。

来看一个例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
function shuffle(arr) {
  return arr.sort(() => Math.random() - 0.5);
}

/**
 * 用于验证 shuffle 方法是否完全随机
 */
function test_shuffle(shuffleFn) {
  // 多次乱序数组的次数
  let n = 100000;
  // 保存每个元素在每个位置上出现的次数
  let countObj = {
    a: Array.from({ length: 10 }).fill(0),
    b: Array.from({ length: 10 }).fill(0),
    c: Array.from({ length: 10 }).fill(0),
    d: Array.from({ length: 10 }).fill(0),
    e: Array.from({ length: 10 }).fill(0),
    f: Array.from({ length: 10 }).fill(0),
    g: Array.from({ length: 10 }).fill(0),
    h: Array.from({ length: 10 }).fill(0),
    i: Array.from({ length: 10 }).fill(0),
    j: Array.from({ length: 10 }).fill(0),
  };
  for (let i = 0; i < n; i++) {
    let arr = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j"];
    shuffleFn(arr);
    countObj.a[arr.indexOf("a")]++;
    countObj.b[arr.indexOf("b")]++;
    countObj.c[arr.indexOf("c")]++;
    countObj.d[arr.indexOf("d")]++;
    countObj.e[arr.indexOf("e")]++;
    countObj.f[arr.indexOf("f")]++;
    countObj.g[arr.indexOf("g")]++;
    countObj.h[arr.indexOf("h")]++;
    countObj.i[arr.indexOf("i")]++;
    countObj.j[arr.indexOf("j")]++;
  }
  console.table(countObj);
}
test_shuffle(shuffle);

在这个例子中，我们定义了两个函数，shuffle 中使用 sort 和 Math.random() 进行数组乱序操作；
test_shuffle 函数定义了一个长度为 10 的数组 [‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’, ‘h’, ‘i’, ‘j’]，并使用传入的乱序函数进行十万次操作，并将数组中每个元素在每个位置出现的次数存放到变量 countObj 中，最终将 countObj 打印出来。
结果如下：

(运行结果)

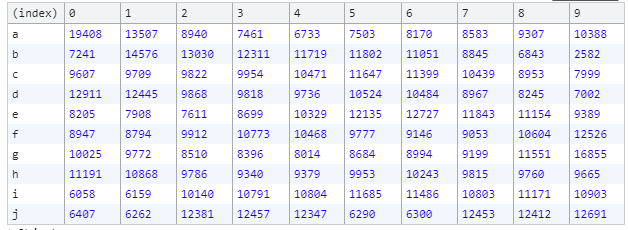
从这个表格中我们能够看出，每个元素在每个位置出现的概率相差很大，比如元素 a ，
在索引 0 的位置上出现了 19408 次，在索引 4 的位置上只出现了 6733 次，
元素 a 在这两个位置出现的次数相差很大（相差一倍还多）。
如果排序真的是随机的，那么每个元素在每个位置出现的概率都应该一样，
实验结果各个位置的数字应该很接近，而不是像现在这样各个位置的数字相差很大。
那么问题出在哪里呢？

插入排序

如果要追究这个问题所在，就必须了解 sort 函数的原理，然而 ECMAScript 只规定了效果，没有规定实现的方式，所以不同浏览器实现的方式还不一样。

为了解决这个问题，我们以 v8 为例，v8 在处理 sort 方法时，使用了插入排序和快排两种方案。 当目标数组长度小于 10 时，使用插入排序；反之，使用快速排序。

源码地址：https://github.com/v8/v8/blob/master/src/js/array.js

为了简化篇幅，我们对 [1, 2, 3] 这个数组进行分析，数组长度为 3，此时采用的是插入排序。

1
2
3
4
5
6
7
8
9
10
11
12
function insertSort(list = []) {
  for (let i = 1, len = list.length; i < len; i++) {
    let j = i - 1;
    let temp = list[i];
    while (j >= 0 && list[j] > temp) {
      list[j + 1] = list[j];
      j = j - 1;
    }
    list[j + 1] = temp;
  }
  return list;
}

其原理在于将第一个元素视为有序序列，遍历数组，将之后的元素依次插入这个构建的有序序列中。
我们来个简单的示意图：

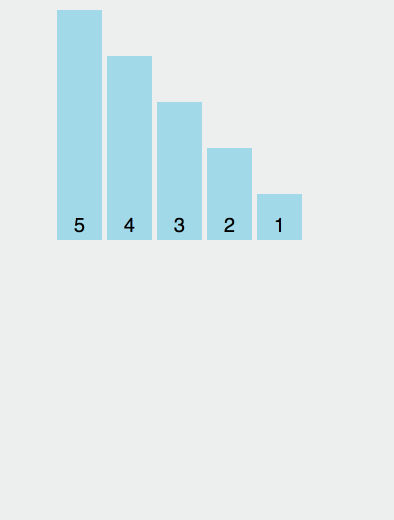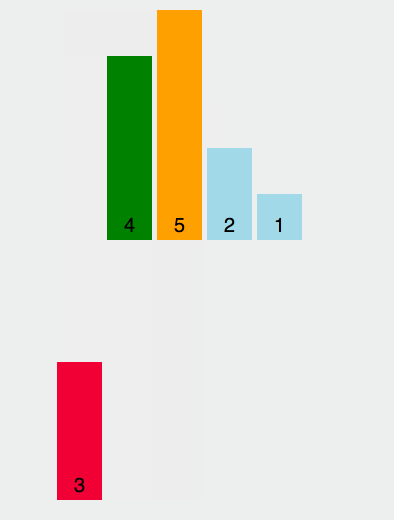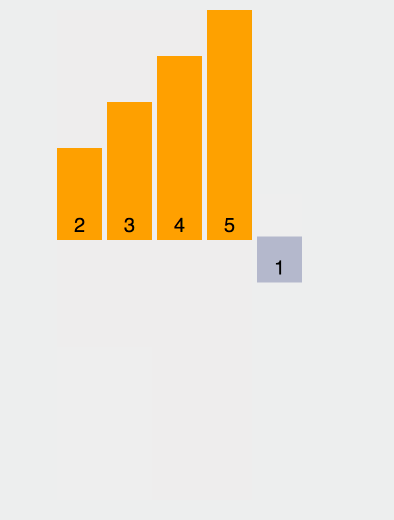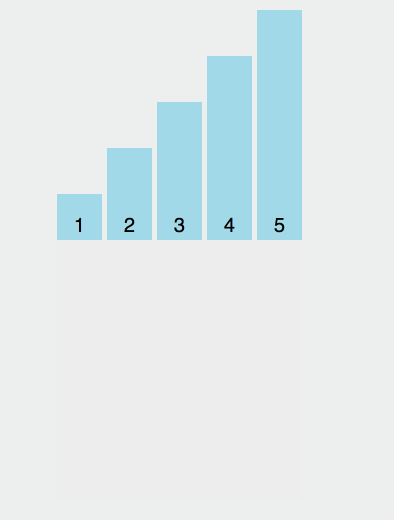
(排序效果图)

现在我们来具体分析[1, 2, 3]这个数组排序；

因为插入排序视第一个元素为有序的，所以数组的外层循环从 i = 1 开始，a[i] 值为 2，此时内层循环遍历，比较 compare(1, 2)，因为 Math.random() - 0.5 的结果有 50% 的概率小于 0 ，有 50% 的概率大于 0，所以有 50% 的概率数组变成 [2, 1, 3]，50% 的结果不变，数组依然为 [1, 2, 3]。

假设依然是 [1, 2, 3]，我们再进行一次分析，接着遍历，i = 2，a[i] 的值为 3，此时内层循环遍历，比较 compare(2, 3)：

有 50% 的概率数组不变，依然是 [1, 2, 3]，然后遍历结束。

有 50% 的概率变成 [1, 3, 2]，因为还没有找到 3 正确的位置，所以还会进行遍历，所以在这 50% 的概率中又会进行一次比较，compare(1, 3)，有 50% 的概率不变，数组为 [1, 3, 2]，此时遍历结束，有 50% 的概率发生变化，数组变成 [3, 1, 2]。

综上，在 [1, 2, 3] 中，有 50% 的概率会变成 [1, 2, 3]，有 25% 的概率会变成 [1, 3, 2]，有 25% 的概率会变成 [3, 1, 2]。

另外一种情况 [2, 1, 3] 与之分析类似，我们将最终的结果汇总成一个表格：

数组 i = 1 i = 2 总计
[1, 2, 3] 50% [1, 2, 3] 50% [1, 2, 3] 25% [1, 2, 3]
25% [1, 3, 2] 12.5% [1, 3, 2]
25% [3, 1, 2] 12.5% [3, 1, 2]
50% [2, 1, 3] 50% [2, 1, 3] 25% [2, 1, 3]
25% [2, 3, 1] 12.5% [2, 3, 1]
25% [3, 2, 1] 12.5% [3, 2, 1]

那么如何高性能的实现真正的乱序呢？而这就要提到经典的 Fisher–Yates 算法。

Fisher–Yates

为什么叫 Fisher–Yates 呢？ 因为这个算法是由 Ronald Fisher 和 Frank Yates 首次提出的。
代码实现：

1
2
3
4
5
6
7
function shuffle(a) {
  for (let i = a.length; i; i--) {
    let j = Math.floor(Math.random() * i);
    [a[i - 1], a[j]] = [a[j], a[i - 1]];
  }
  return a;
}

原理很简单，就是遍历数组元素，然后将当前元素与以后随机位置的元素进行交换，从代码中也可以看出，这样乱序的就会更加彻底。

测试代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
var times = 100000;
var res = {};

for (var i = 0; i < times; i++) {
  var arr = shuffle([1, 2, 3, 4]);

  var key = JSON.stringify(arr);
  res[key] ? res[key]++ : (res[key] = 1);
}

// 为了方便展示，转换成百分比
for (var key in res) {
  res[key] = (res[key] / times) * 100 + "%";
}

console.log(res);
// 测试结果如下
{
  [1,2,3]: "16.667%",
  [1,3,2]: "16.761%",
  [2,1,3]: "16.636%",
  [2,3,1]: "16.624%",
  [3,1,2]: "16.744%",
  [3,2,1]: "16.567999999999998%",
}

从测试结果我们可以看出，每个元素在每个位置出现的次数相差不大，说明这种方式满足了随机性的要求。
而且 Fisher–Yates 算法只需要通过一次遍历即可将数组随机打乱顺序，性能极为优异~~
至此，我们找到了将数组乱序操作的最优办法：Fisher–Yates~

参考文献